什么是贝叶斯定理?
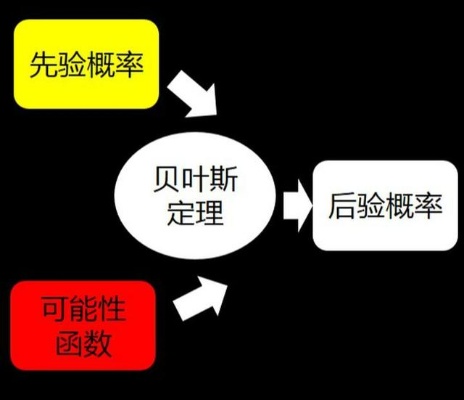
贝叶斯定理的应用
贝叶斯定理在机器学习中的应用
如何使用贝叶斯定理进行分类
贝叶斯定理的优缺点
如何避免贝叶斯陷阱
贝叶斯定理是一种概率理论,可用于在给定先验知识的情况下,通过新的证据来更新概率。它是机器学习中的重要算法之一,尤其在分类问题中广泛应用。
什么是贝叶斯定理?
贝叶斯定理是一种基于概率的算法,用于计算给定某些证据情况下某一假设的概率。它由英国数学家托马斯·贝叶斯于18世纪提出,被广泛应用于统计学、人工智能和机器学习领域。
贝叶斯定理的应用
贝叶斯定理可以用于预测未来事件的概率,例如天气预报、股票价格预测等。此外,它还可以用于过滤垃圾邮件、语音识别、图像识别等应用。
贝叶斯定理在机器学习中的应用
贝叶斯定理在机器学习中的应用非常广泛,尤其是在分类问题中。它可以用于文本分类、垃圾邮件过滤、情感分析等应用。
如何使用贝叶斯定理进行分类
使用贝叶斯定理进行分类的过程包括以下几个步骤:
1. 收集数据集并将其分为训练集和测试集。
2. 计算每个类别的先验概率。
3. 对于每个特征,计算在每个类别中的条件概率。
4. 对于测试样本,计算其在每个类别中的后验概率。
5. 将测试样本分配给具有最高后验概率的类别。
贝叶斯定理的优缺点
贝叶斯定理的优点包括:
1. 算法简单易懂。
2. 可以处理高维数据。
3. 可以处理缺失数据。
贝叶斯定理的缺点包括:
1. 假设特征之间相互独立,但实际上很少存在这种情况。
2. 需要大量的数据来训练模型。
如何避免贝叶斯陷阱
贝叶斯陷阱指的是在计算后验概率时,如果某个特征在训练集中从未出现过,则它在计算条件概率时会变为0,导致后验概率为0。为了避免贝叶斯陷阱,可以使用平滑技术,例如拉普拉斯平滑或贝叶斯平滑。
贝叶斯定理是机器学习中的重要算法之一,尤其在分类问题中广泛应用。虽然它有一些缺点,但它的优点使得它在实际应用中得到了广泛的应用。








