telligence，简称AI）是指通过计算机模拟人类智能的理论、方法、技术和应用系统的总和。在人工智能的研究和应用中，数学是一个不可或缺的基础。本文将深入探讨人工智能中的数学原理。
一、概率论
概率论是人工智能中最基础的数学学科之一，主要用于描述不确定性。在人工智能领域，概率论被广泛应用于机器学习、数据挖掘、自然语言处理等方面。在机器学习中，贝叶斯网络就是基于概率论的一种模型，可以用于处理分类、聚类、回归等任务。
二、线性代数
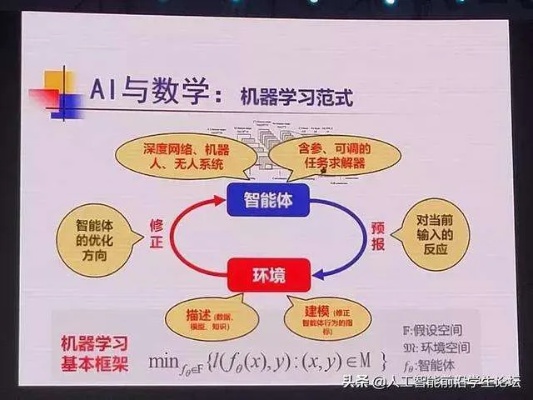
线性代数是人工智能中另一个基础学科，主要用于描述向量和矩阵之间的运算关系。线性代数被广泛应用于神经网络、图像处理、自然语言处理等方面。在神经网络中，线性代数可以用于描述神经元之间的连接关系和权重。
三、微积分
微积分是人工智能中的另一个重要学科，主要用于描述函数的变化规律。微积分被广泛应用于优化算法、机器学习等方面。在优化算法中，梯度下降法就是基于微积分的一种算法，用于寻找函数的最小值。
四、信息论
信息论是人工智能中的一个重要学科，主要用于描述信息的传输和处理。信息论被广泛应用于数据压缩、信号处理、语音识别等方面。在语音识别中，信息论可以用于描述语音信号的频率和幅度等特征。
总之，数学是人工智能的重要基础，各个数学学科在人工智能中都有着广泛的应用。未来，随着人工智能技术的不断发展，数学在人工智能中的作用将会变得越来越重要。
版权声明：
内容均收集于互联网,有侵权或不妥之处,请联系我们删除。敬请谅解！
